
BinaryTree(이진트리) 가 무엇인가?
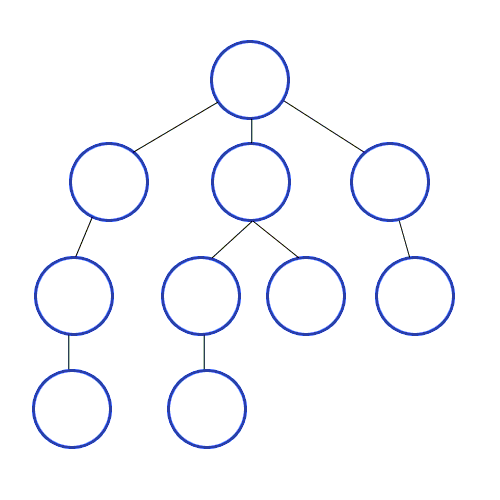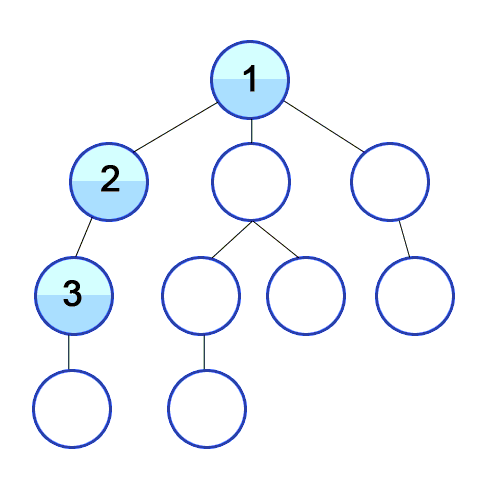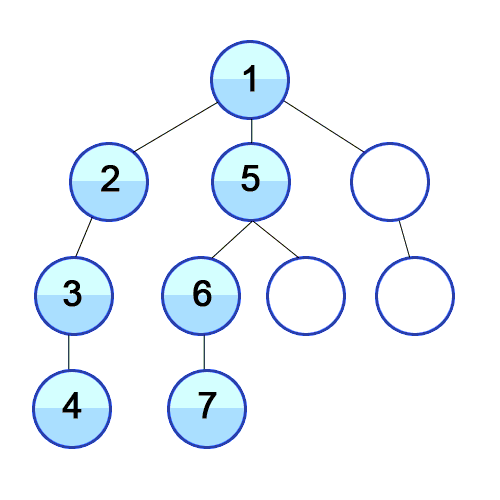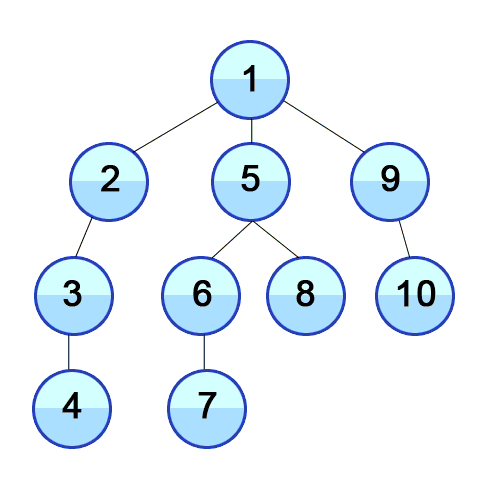
이진트리는 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 노드 자식 노드라고 한다.

그림에서 보면 다음과 같은 규칙을 가지고 있다.
- 이진트리는 항상 두개의 자식 노드를 가지고 있다.
- 모든 원소는 중복된 값을 가져서는 안된다.
- 왼쪽 서브트리에 존재하는 노드들의 값은 그 트리의 루트 값보다 반드시 작다.
- 오른쪽 서브트리에 존재하는 노드들의 값은 그 트리의 루트 값보다 반드시 크다.
이진트리의 종류

모든 레벨의 노드가 꽉 차있는 이진트리
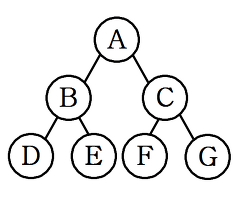
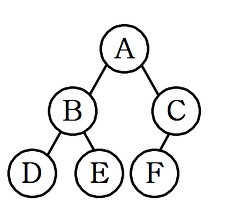
완전 이진 트리 (무조건 왼쪽부터 차곡차곡 채워진 형태)
이진트리의 삽입 예시

그렇다면 이진트리를 왜 사용할까?
이진트리(Binary search tree) 와 정렬된 배열 (Sorted array) 의 선형 자료 구조 을 예시로 보자.

각각의 스텝 수를 보면 알 수 있다시피, 값을 찾는데 있어서 이진트리가 훨씬 빠르다.
트리 자료구조는 탐색에 걸리는 시간이 O(log n) 인 반면
선형 자료구조는 탐색에 걸리는 시간이 O(n)이다.
이진트리 순회 종류
전위 순회법(Preorder Traversal)
- 루트 노드부터 시작해서 아래로 내려 오면서
- 왼쪽 하위 트리를 방문하고 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위 트리를 방문하는 방식

중위 순회법(Inorder Traversal)
트리는 하위 트리의 집합이라고 할 수 있고 하위 트리 역시 또 다른 하위 트리의 집합이라고 할 수 있다.
따라서 아래와 같은 방법으로 탐색할 수 있다.
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문하는 방법

응용 사례 : 수식 트리(Expression Tree), 중위 표기식
(1 * 2) + (7 - 8)을 수식 트리로 표현하면 다음 그림과 같이 나타낼 수 있다.

후위 순회법(Postorder Traversal)
전위 순회의 반대
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 형제 노드를 방문 후
- 루트 노드를 방문하는 방법.

응용 사례 : 후위 표기식.
후위 순회법을 통해 출력되는 노드를 살펴보면 후위 표기식으로 나타난다.
- 1 2 * 7 8 - +

DFS (Depth FIrst Search)
깊이 우선 탐색을 의미한다.
Root Node 혹은 다른 임의의 Node 로 부터 한줄 한줄 완벽하게 탐색하는 방법이다.
따라서 모든 노드를 방문하는 경우에 사용하는 방법이기도 하다.
Stack 또는 Recursion(재귀함수) 으로 구현된다고 한다.
- 시간 복잡도
- 접점 (V), 간선(E)
- 인접리스트 : O(V + E)
- 인접 행렬 : O(V^2)
BFS (Breadth-first-search)
Root Node 혹은 다른 임의의 노드에서 인접한 노드를 먼저 탐색하는 방법이다.
보통 Queue를 사용해서 구현한다.

- 시간 복잡도
- 접점 (V), 간선(E)
- 인접리스트 : O(V + E)
- 인접 행렬 : O(V^2)
균형잡힌 이진탐색트리
노드가 추가, 삭제될 때, 트리의 균형상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 트리이다.
다음과 같이 편향된 상태의 이진탐색트리가 계속 편향 된다면, 데이터의 탐색 수행시간이 O(log n)이 아니라 O(n)에 가까워질 것이다.

즉, 시간 복잡도를 줄이기 위해서 편향된 이진탐색트리의 균형을 잡아주는 것이 중요하다.

균형잡힌 이진탐색트리의 종류중 가장 유명한 것은 AVL Tree , Red-Black Tree가 있다.
AVL Tree

균형 인수 = 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이
균형 인수의 절댓값이 크면 클수록 균형이 무너진 상태, 절댓값이 2 이상인 경우 트리 재조정 진행
Red-Black Tree


참고로 자바에서 사용하는 Tree는 Red-Black Tree 기반이다.

힙
heap 자료구조를 사용하여 자료내에서 최댓값과 최솟값을 빠르게 찾아낼 수 있다.
완전 이진트리를 사용한 자료구조이다. 부모노드는 항상 자식 노드보다 우선순위에 있게된다.

자바에서는 다음의 heap자료구조를 PriorityQueue<T> 라는 이름으로 구현해 놓았다.
출처:
'스터디 > [white-ship] 자바 스터디(study hale)' 카테고리의 다른 글
| 4주차 과제: Queue (0) | 2021.01.02 |
|---|---|
| 5주차 과제: 클래스 (0) | 2021.01.01 |
| 7주차 과제: 패키지 (0) | 2021.01.01 |
| 5주차 과제: BinaryTree 실습 (0) | 2021.01.01 |
| 0주차 : kick off (0) | 2020.12.26 |




댓글